问题描述
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
示例 1
输入: "babad"
输出: "bab"
注意: "aba" 也是一个有效答案。
示例 2
输入: "cbbd"
输出: "bb"
什么是回文
回文是一个正读和反读都相同的字符串,例如,”aba” 是回文,而 “abc” 不是。
暴力解法
最容易想到的方法就是遍历所有字符串,检测是否为回文子串,时间复杂度为 O(n^3),通过下面的优化,勉强可以通过 LeetCode。
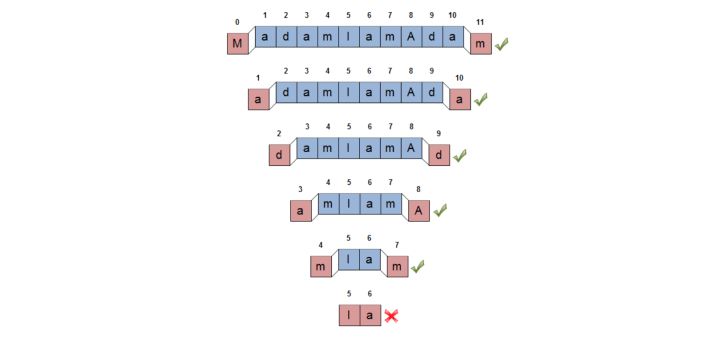
- 从最长字符串开始遍历,一旦找到回文子串,立即返回。
- 判断是否回文使用收缩法,从最外一堆字符向中心推进
Swift 实现
class Solution {
func longestPalindrome(_ s: String) -> String {
let arr = Array(s)
var size = arr.count
while size > 0 {
var low = 0
var high = low + size - 1
while high < arr.count {
if isPalindrome(arr, low: low, high: high) {
return String(arr[low...high])
}
low += 1
high += 1
}
size -= 1
}
return ""
}
func isPalindrome(_ s:[Character], low:Int, high:Int) -> Bool {
var l = low, h = high
while l <= h {
if s[l] == s[h] {
l += 1
h -= 1
} else {
return false
}
}
return true
}
}
中心扩展算法
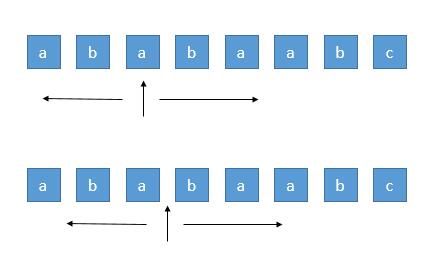
回文串一定是对称的,所以我们可以每次循环选择一个中心点,进行左右扩展,判断左右字符是否相等即可。
字符串个数为奇数时总共有 n 个中心点,偶数时有 n - 1 个中心点,所以中心点会有 2n - 1 个,时间复杂度为 O(n^2)。
Swift 实现
class Solution {
func longestPalindrome(_ s: String) -> String {
if s.count <= 1 {
return s
}
let arr = Array(s)
var start = 0, end = 0
for i in 0..<arr.count {
let len1 = expand(arr, i, i)
let len2 = expand(arr, i, i + 1)
let len = max(len1, len2)
if len > end - start + 1 {
start = i - (len - 1)/2
end = i + len/2
}
}
return String(arr[start...end])
}
func expand(_ s:[Character], _ low:Int, _ high:Int) -> Int {
var l = low, h = high
while l >= 0 && h < s.count && s[l] == s[h]{
l -= 1
h += 1
}
return h - l - 1
}
}
文档信息
- 本文作者:Ning Zhang
- 本文链接:https://sunsetroads.github.io/2018/06/18/longest-palindrome/
- 版权声明:自由转载-非商用-非衍生-保持署名(创意共享3.0许可证)